We may think we know Galileo Galilei, the 17th century scientist and Renaissance man. We probably learned at some point in our education that he discovered the moons of Jupiter using a telescope he invented, and he upended Aristotle by working out the laws of falling objects. Challenging Church authority, he promoted the Copernican view that the Sun, not the Earth, was the center of the known universe. Less appreciated is that none of his breakthroughs came all at once. Each involved experimenting, making mistakes, and revising assumptions. But that’s the way science works.
◊
Galileo was an entrepreneur, philosopher, experimental physicist, and astronomer. The more I delved into his life, the more surprised I was. It turns out he was in some ways a familiar figure. As an early 17th-century “tech entrepreneur,” he invented and sold a calculating device that was the forerunner to the slide ruler. And, Galileo’s then unique philosophy of theorizing and measuring results, what we call today the scientific method, led him to other major discoveries and more inventions.
We moderns are inheritors of this tradition. We take for granted the laws and principles that Galileo and other early scientists struggled to derive; convincing the rest of the world of their truth was an additional challenge. Even today if we asked a random person on the street whether a 30-pound lead weight falls faster than a 10-pound one, would we be surprised if they gave the wrong answer? It’s a trick question for many, since Galileo taught us they both fall at the same speed.
“Poetry, mythology, and religion represent the world as man would like to have it, while science represents the world as he gradually comes to discover it.” —Joseph Wood Krutch, writer and conservationist
We’d like our intuition to be right, but more often than not it’s wrong. And it was up to Renaissance scientists like Galileo and Kepler, and the later Enlightenment era giants, to reveal the way the universe ticks: not through non-repeatable revelation, but in rhythm with deeper theories that explain what we see, ideas that can be understood and tested by anyone.
Watch "The Cosmos" on MagellanTV now.
Student of Euclid, Challenger of Aristotle
As with all great scientific radicals, Galileo’s ideas and tools of the trade had foundations in the work of earlier masters. For Galileo and his Renaissance peers, their conceptual framework owed everything to the Greeks – particularly Archimedes, the brilliant astronomer Thales of Miletus, and above all the geometer Euclid, the bane of junior high-school students everywhere.
It was Euclid who gave Galileo the gift of similar triangles, which allowed him to make arguments about distance and velocity without using equations. Thanks to the Internet, we can all gaze at the original notes for his great early work De Motu (On Motion) and see that Galileo’s analysis is of the familiar geometric reasoning of “this is to that as that is to this.” In short, Galileo used triangles and circles and discussed ratios between them to make his case.
Aristotle, the Western world’s first scientist, was Galileo’s other lodestar. His principles of motion were a starting point for Galileo, though he’d eventually show them to be incorrect. Aristotle had said that heavier objects fall faster than lighter ones, and that a falling object has a speed proportional to the distance traveled. Wrong, and wrong.
It was far easier for Galileo to analyze and disprove Aristotle’s heavier-objects-fall-faster fallacy than to discover the more subtle relationship between distance and velocity in free fall. Contrary to the popular myth involving a famous leaning tower, instead of first physically dropping cannonballs of different weights, he conducted a thought experiment – Tower of Pisa not needed – in which he imagined a heavier and lighter ball tied together.
What would the velocity be for the combined weights? He first made the case for an average of the two separate velocities – not as fast as the heavier ball, yet not as slow as the lighter one. But then the combined object, according to Aristotle, would now be heavier than either one separately and so should fall faster. It’s a clear contradiction so Aristotle appears to be wrong.
Galileo concluded that all things fall at the same rate. It was not enough to prove Aristotle wrong with logic, Galileo tried it out on his own as in the legend. Reading about his methods, you get a sense of his very modern approach to science: Theorize, then test.
Galileo the Tech Entrepreneur
When Galileo started out, he was poor. His father wanted him to be a doctor – some things never change – but during his university studies in Pisa, he became interested in mathematics and natural philosophy, which was how physics was referred to at the time.
To supplement his small teaching income as a professor, he invented and sold an all-purpose calculating and measuring device (below). It was really an innovative combination of several other 16th-century gadgets – primarily a far improved version of the older proportional compass, which could perform basic multiplication and division, along with a military compass to help site cannons and measure angles for triangulations.
The key concept behind the sector is that you can multiply and divide numbers using similar triangles. Remember from geometry class that when two similar triangles are in a proportion of, say, 7:1, then each side of one triangle is seven times larger than the same side on the other? If not, then take my word for it for now (and then Google it). Galileo was quick to realize that he had an analog way to multiply and divide.

Detail of Galileo’s Compass
(Image Credit: Sage Ross)
How is this done? With Galileo’s compass, you find two numbers on the arithmetic scale on the arm in the proportions you’re interested in, say 20 and 140. To multiply the number 28 by 7, you use the caliper to measure 28 on the arithmetic scale and extend the arms by that distance from the number 20. Then use the calipers again to measure the distance between the arms at 140, forming a side of the proportionally larger triangle, and there you have the answer. Eureka! A computing gadget with no batteries or LEDs.
Galileo also made clever use of additional scales on the sector’s arms for square, cube root, and trigonometric calculations. Essentially, you could do algebra without equations. As we’ll soon see, geometry was also critical in his arguments to discover the laws of motion.
Galileo’s Circle and Disproving Aristotle
I remember being taught that Galileo worked out the famous time-squared formula for free fall by using a ramp to slow the speed of the fall and allow the ball to be more easily timed. True enough. There are plenty of online videos showing high-school students measuring a ball rolling down a ramp. You can watch and learn without doing it yourself.
The impression we all got from our teachers was that Galileo just did the experiment. However, he did not get to this particular experiment without first devising a series of geometric thought experiments. In his first study on inclined planes reported in De Motu, he came to different conclusions.
Galileo was attempting to find a relationship between the time it took for a ball to roll down ramps at different angles and lengths. While his assumptions about falling objects were still based on Aristotle’s principles, he ended up accidentally discovering something called Galileo’s Circle.
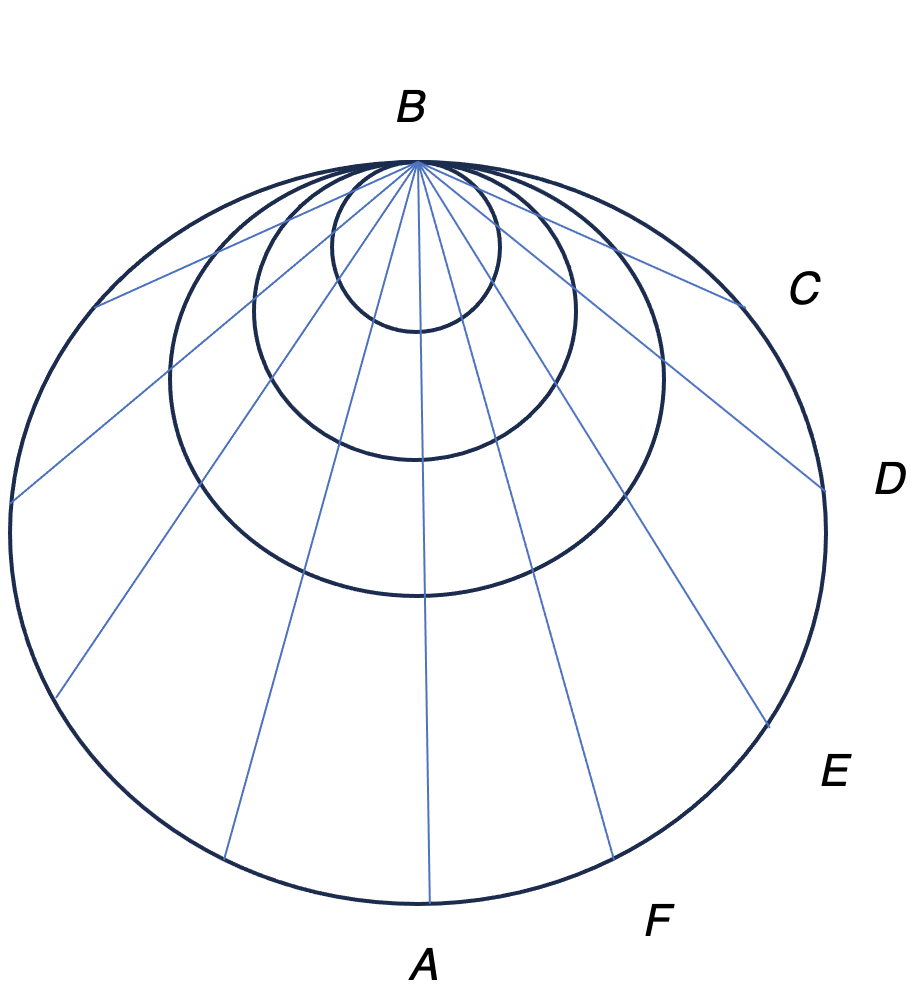
Travel time along the chords of the circle are all the same. Not intuitive!
(Image courtesy of MagellanTV)
Using just geometry, he was able to show that balls dropped directly from B (above) will reach C, D, or any of the lettered points, all at the same time even though they have different distances to travel. The man or woman on the street today, as well as yours truly, would be just as surprised as Galileo was when he first came up with and then demonstrated this idea. It’s not intuitive at all.
Eventually, Galileo did discover the time-squared law of free fall and constant acceleration of gravity, and was able to re-prove his initial experiments with the correct physics. If you’re curious about why Galileo’s Circle works, it’s because in this special setup the average velocity on each of the chords is proportional to the distance covered and so the times are the same. You can learn more here.
Interestingly, there’s a practical value to this equal-time characteristic of Galileo’s Circle. He had long noticed that a gently swinging church chandelier always took the same amount of time for each swing. With the Circle in mind, he later tried to prove what was true for chords of a circle was the same for a slightly perturbed pendulum covering the same arc. Not quite, but the swings were close enough in time to make a gadget that takes advantage of this behavior.
Toward the end of his life, Galileo designed the first grandfather clock with its signature swinging pendulum, which was ultimately built by the 17th-century Dutch physicist and mathematician Christiaan Huygen. Pendulum clocks remained the most accurate time mechanism till the early 20th century.
Modern Science vs. Religion
Scientists can be wrong. That is as it should be. But through testing and further intellectual refinements, they’re always getting closer to the truth.
The Galileo propositions about inertia, free-fall, and momentum that we all learned somewhere in high school or college came from a later work, known as the Discourses on Two New Sciences. The Discorsi was published about 1638 and written in Italian, not Latin. It was an explanation in dialogue form, theorems included, of everything he had learned over a lifetime of study and experiments. With its Copernican view, it was the work that finally earned him the attention of the Roman Inquisition.
Religious fundamentalists today (and in the past) find this trial-and-error approach of science to be a major flaw. After all, the complete truth of the world has been received from the ultimate source, and it can never be wrong. In their minds, when scientists change their theories – because of new facts or mistaken assumptions – they’re admitting that they’re not infallible. But that, in fact, is the essence of science.
According to legend, the pope at the time of Galileo’s trial for heresy, Urban VII, refused to look through the newly invented telescope to see the moons of Jupiter. Historians tell us this meeting and refusal likely never happened.
But certainly his more religious friends were uncomfortable. We know from letters that his philosopher friend Cesare Cremonini didn’t need to see the heavens through Galileo’s spyglass. Cremonini already knew the answer from Aristotle: The celestial realm consisted of perfect spheres.
Unfortunately, it’s a sentiment not that different from a new generation of the conspiracy-minded who believe, without evidence, whatever an “authority” tells them. Science’s victories have never and will never come easily.
Ω
(Title Image Credit: Lucas Pezeta, via Pexels)

